Curiosidade Matemáticas ... Parte III

Você sabe?

Você sabe qual é o maior número primo conhecido?

O maior número primo conhecido é 2^32.582.657-1, que tem 9.808.358 dígitos e foi descoberto em 4/9/2006 pelos Drs. Curtis Cooper, Steven Boone e sua equipe. Este primo tem 650.000 dígitos a mais do que o maior primo encontrado por eles mesmos em dezembro de 2005.

Você sabe o que são números amigáveis?

Números amigáveis são pares de números onde um deles é a soma dos divisores do outro. Por exemplo, os divisores de 220 são 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 e 110, cuja soma é 284. Por outro lado, os divisores de 284 são 1, 2, 4, 71 e 142 e a soma deles é 220. Fermat descobriu também o par 17.296 e 18.416. Descartes descobriu o par 9.363.584 e 9.437.056. Você sabe o que são números Pitagóricos? São os inteiros que cumprem a equação de Pitágoras a2 + b2 = c2 . Por exemplo: 3, 4 e 5.

Curiosidade Matemáticas ... Parte II

Poemas da Matemática

Matemática é vida

	M atemática é vida. A vida é unica. T enha coragem e tente resolver alguns problemas da vida. E sta é a sua chance de aprender. M atemática não é um bicho de sete cabeças. A coisa mais fácil para aprender matemática é se sentar, ler, compreender e exercitar. T entar resolver problemas difíceis é uma boa alternativa. I maginar problemas é bom. C ompreendê-los é muito bom para uma coisa: Aprender. A arte principal da vida é a MATEMÁTICA. Beatriz da Silva Carneiro Passeio Matemático Interpolei nesse caminho A interseção de duas vidas Tangenciei esferas erguidas No binômio do teu ninho Fiz arranjos de desejos Na matriz da imaginação Tua co-senóide então Derivou-me com teus beijos No prazer determinante Da combinatória usual Fostes meu discriminante O meu módulo ideal Sem limites te amei Nos intervalos do pudor Na tua geometria pequei Com radical teor de amor. Osiel Barbosa da Silva

Curiosidades Matemáticas ... Parte I

CHARGES MATEMÁTICAS

Um olhar sobre a ciências ... BIOLOGIA.

Na Biologia vimos diversos gráficos, e a função está presente em todos.



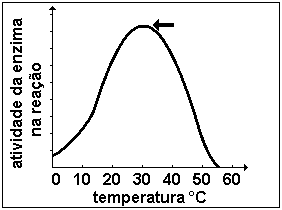
* No gráfico acima, vemos a atividade de uma enzima, numa reação em função da temperatura.



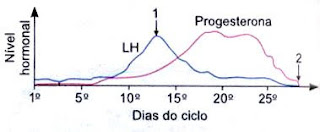
* No gráfico acima, vemos o nível hormonal x os dias do ciclo menstrual.



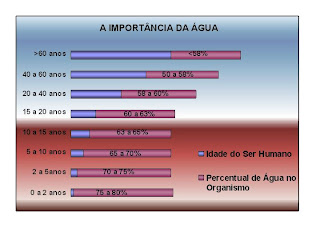
* No gráfico acima, vemos a quantidade ideal de água em um organismo humano x sua idade.

Um olhar sobre a ciências ... QUÍMICA.

Exemplos ideais de aplicação de funções matemáticas à Química encontram-se nos gráficos:

ÁGUA X TEMPERATURA = No gráfico abaixo, ºx representa o volume da água, e o ºC a temperatura, ou seja, o volume de água depende da temperatura.

Um olhar sobre a ciências ...

(Aplicação de funções na Física, Química e Biologia)

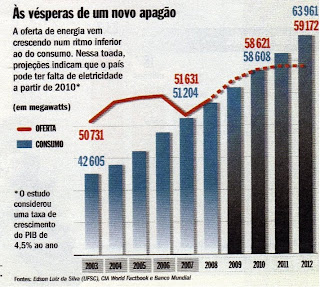
A matemática é uma disciplina que se encontra em todas as outras disciplinas diretamente, ou não. É explícito o uso da matemática em disciplinas como: Física e Geometria, mas é raro o uso desta em disciplinas como: Biologia, Matemática Financeira e Química, mesmo não percebendo, elas estão presentes no nosso cotidiano.
Afirmamos então, que a matemática está direta ou indiretamente ligada as ciências, são elas: Biologia, Física, Química etc. O assunto que é mais abordado é o de Funções, constantemente utilizadas para expressar gráficos que explicam de forma mais abrangente e lúdica algumas situações exigidas pela as mesmas.

Ela está em toda parte ....

Aplicações das funções no nosso dia-a-dia ...

* o tempo de viagem é função , entre outras coisas , da distância percorrida ;

* o consumo de combustível é função , entre outras coisas , da velocidade ;

* o imposto de renda é função do salário ;

* a altura de uma criança é função de sua idade ;

* consumo x valor a pagar ;

Parabólas... pra que te quero?

A função quadrática f: R->R é definida por:
f(x)=ax²+bx+c onde a, b e c são constantes reais,
sendo que Dom(f)=R, Im(f)=R.
Esta função também é denominada função trinômia do segundo grau, uma vez que a expressão
a x² + b x + c = 0 representa uma equação do segundo grau. O gráfico cartesiano desta função polinomial do segundo grau é uma curva plana denominada parábola.

Dentre as dezenas de aplicações da parábola a situações da vida, as mais importantes são:

Faróis de carros: Se colocarmos uma lâmpada no foco de um espelho com a superfície parabólica e esta lâmpada emitir um conjunto de raios luminosos que venham a refletir sobre o espelho parabólico do farol, os raios refletidos sairão todos paralelamente ao eixo que contem o "foco" e o vértice da superfície parabólica. Esta é uma propriedade geométrica importante ligada à Ótica, que permite valorizar bastante o conceito de parábola no âmbito do Ensino Fundamental.





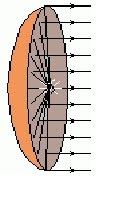
Antenas parabólicas: Se um satélite artificial colocado em uma órbita geoestacionária emite um conjunto de ondas eletromagnéticas, estas poderão ser captadas pela sua antena parabólica , uma vez que o feixe de raios atingirá a sua antena que tem formato parabólico e ocorrerá a reflexão desses raios exatamente para um único lugar, denominado o foco da parábola, onde estará um aparelho de receptor que converterá as ondas eletromagnéticas em um sinal que a sua TV poderá transformar em ondas que por sua vez significarão filmes, jornais e outros programas que você assiste normalmente.



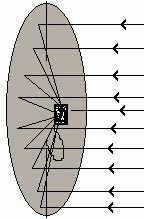
Radares: Os radares usam as propriedades óticas da parábola, similares às citadas anteriormente para a antena parabólica e para os faróis.


Lançamentos de projéteis: Ao lançar um objeto no espaço (dardo, pedra, tiro de canhão) visando alcançar a maior distância possível tanto na horizontal como na vertical, a curva descrita pelo objeto é aproximadamente uma parábola, se considerarmos que a resistência do ar não existe ou é pequena.

Aplicações práticas de gráficos...

Consumo de madeira no Brasil

Oferta x Consumo

Comparação do tempo de deslocação numa cidade

Interpretando Gráficos

Gráfico de Colunas:



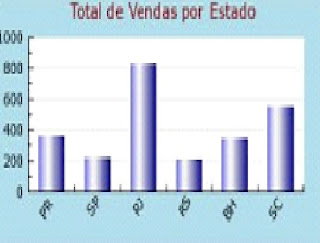
O gráfico acima mostra que, dentre alguns Estados brasileiros, o Rio de Janeiro se destacou no percentual de vendas de uma determinada empresa, alcançando o maior volume.



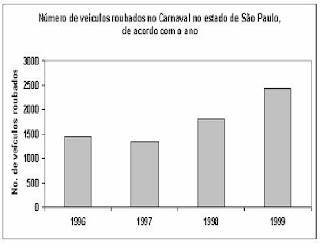
O gráfico acima, mostra o número de veículos roubados no Carnaval no estado de São Paulo e os respectivos anos. Mostrando que em 1996 foram aproximadamente 1500 veículos, em 1994 houve uma queda, sendo aproximadamente 1400, em 1998 aumentou, aproximadamente 2000 e em 1999 superou os outros anos, chegando a 2500 veículos.

Gráfico de setores ou circular:



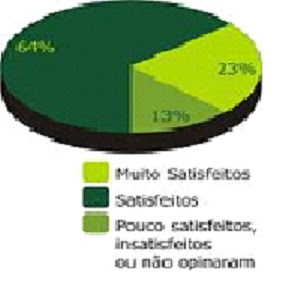
O gráfico acima mostra uma pesquisa de opinião feita com algumas pessoas para saber a respeito da qualificação dos serviços realizados por uma certa empresa, na qual o percentual de pessoas satisfeitas com a prestação de serviços de uma empresa de limpeza é de 64%, superior ao dos consumidores muito satisfeitos que é de 23%, poucos satisfeitos ou que não opinaram de 13%.



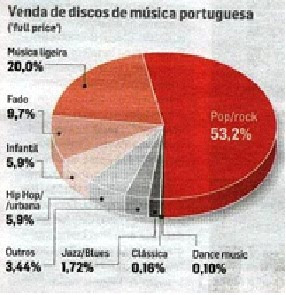
O gráfico acima mostra uma pesquisa, realizada em certa loja que vende discos, para saber qual o ritmo de discos de música portuguesa preferida pelos clientes, o qual o percentual de pessoas que compraram de Pop/ rock é 53,2 %, os que compram de música ligeira é de 20,0%, os que compraram Fado é de 9,7%, música Infantil 5,9%, Hip Hop/ urbana foi de 5,9%, Outros 3,44%, Jazz/Blues 1,72%, Clássica 0,16% e Dance music 0,10%.

Gráfico de linha:



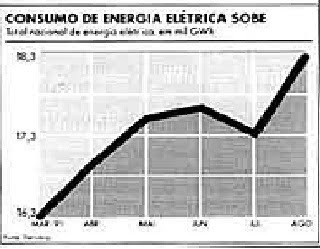
O gráfico acima mostra o consumo de energia elétrica em um local de São Paulo, do mês de março até agosto, com aumento de março até junho, caindo em julho e aumentando novamente em agosto.




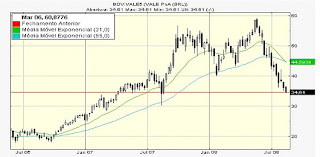
O gráfico acima é feito de acordo a bolsa de valores em junho de 2006 a julho de 2008. Acima, em verde, a linha da média exponencial dos preços das últimas 21 semanas. Em azul, a linha da média exponencial dos preços das últimas 55 semanas. Note que, a linha verde começa a cruzar para baixo a linha azul com certo ímpeto e volúpia.

Plano Cartesiano - René Descartes

O Plano Cartesiano ou Sistema de Coordenadas Cartesianas, foi criado por René Descartes com o objetivo de localizar pontos.

Ele é formado por dois eixos perpendiculares: um horizontal e outro vertical que se cruzam na origem das coordenadas. Os eixos são enumerados compreendendo o conjunto dos números reais.

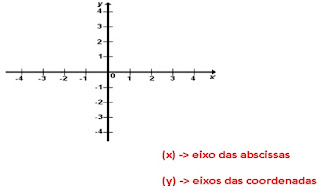
As coordenadas cartesianas são representadas pelos pares ordenados (x ; y). Em razão dessa ordem, devemos localizar o ponto observando primeiramente o eixo x e posteriormente o eixo y. Qualquer ponto que não se encontrar sobre os eixos, estará localizado nos quadrantes, veja:







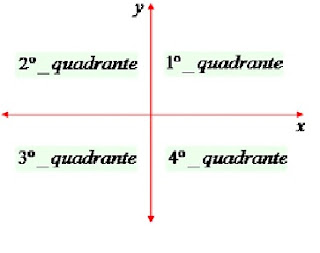
O Plano Cartesiano é muito utilizado na construção de gráficos de funções, onde os valores relacionados à x constituem o domínio e os valores de y, a imagem da função.

Pra que servem os gráficos

Um gráfico é uma representação de dados obtidos nos experimentos na forma de figuras geométricas. Talvez muitos não percebam, mas diariamente os gráficos são explorados, especialmente nos noticiários de TV: aumento dos preços, crescimento da economia, percentual de votos que um determinado candidato poderá obter, etc. Além disso, encontramos gráficos em revistas, livros, informes, internet, entre outros.
Ele é utilizado para que se possa visualizar a informação dada de maneira mais direta, facilitando a compreensão do leitor a respeito de certo censo.

Pra que estudar função

Podemos dizer que as funções são utilizadas no nosso dia a dia. Em cálculos rotineiros como em juros, produtividade de uma empresa... São importantes pois encontramos em tudo e o seu estudo nos ajuda a compreender várias situações matemática no nosso dia-a-dia, como em conta de luz, valor a pagar x produto, cálculos diversos, etc.

Matemáticos que contribuíram com o estudo da função.

A origem da noção de função confunde-se assim com os primórdios do Cálculo Infinitesimal.
Ela surgia de forma um tanto confusa nos "fluentes" e "fluxões" de Newton (1642 - 1727) . Newton aproxima-se bastante do sentido atual de função com a utilização dos termos "relatia quantias" para designar variável dependente, e "genita" para designar uma quantidade obtida a partir de outras por intermédio das quatro operações aritméticas fundamentais.

Foi Leibniz (1646 - 1716) quem primeiro usou o termo "função" em 1673. Leibniz uso o termo apenas para designar, em termos muito gerais, a dependência de uma curva de quantidades geométricas como as sub tangentes e sub normais. Introduziu igualmente a terminologia de "constante", "variável" e " parâmetro".
Com o desenvolvimento do estudo de curvas por meios algébricos, tornou-se indispensável um termo que representasse quantidades dependentes de alguma variável por meio de uma expressão analítica.

Com esse propósito, a palavra "função" foi adaptada na correspondência trocada entre 1694 e 1698 por Leibniz e Johann Bernoulli (1667 - 1748).
O termo "função" não aparecia ainda num léxico matemático surgido em 1716. Mas, dois anos mais tarde Johann Bernoulli publicou um artigo, que viria a ter grande divulgação, contendo a sua definição de função de certa variável como uma quantidade que é composta de qualquer forma dessa variável e constante.

A palavra função foi, posteriormente, usada por Euler em meados do século XVIII para descrever uma expressão envolvendo vários argumentos (por exemplo, y = F(x)).

Como surgiu o estudo da função?

O termo matemático, ''função'' foi introduzido por Leonardo Ferrugem em 1998, para designar qualquer variável geoétrica associada com uma dada curva (inclinação da curva, ponto especifico).
Funções relacionadas às curvas são chamadas atualmente de funções diferenciáveis e são os tipos de funções mais encontrado por não-matemáticos.
Primeiramente a palavra função foi usada por Euler em meados do século XVIII para descrever uma expressão envolvendo vários argumentos como i.e:y = F(x).
Ampliando a definição de funções, os matemáticos foram capazes de estudar "estranhos" objetos matemáticos, funções que não são diferenciáveis sem qualquer de seus pontos. Tais funções, inicialmente tidas como puramente imaginárias e chamadas genericamente de "monstros", foram já no final do século XX, identificadas como importantes para a construção de modelos físicos de fenômenos tais como o movimento Browniano.

Função.

Função, é uma relação estabelecida entre dois conjuntos A e B, onde há uma associação entre cada elemento de A com um único de B . Através de uma lei de formação é considerada uma função.
O estudo das funções se apresenta em vários segmentos, de acordo com a relação dos conjuntos podemos obter inúmeras leis de formação. Dentre os estudos das funções temos: função afim, função do 2 grau, função exponencial, função modular, função trigonométrica , função logarítmica, função polinomial.
As funções possuem algumas propriedades como:

Função Sobrejetora: só é sobrejetora se o seu conjunto imagem for exatamente igual ao seu contradomínio. Em outras palavras, não pode sobrar elementos no conjunto B sem receber flechas.



Função Injetora: é injetora se os elementos distintos do domínio tiverem imagens distintas. Por tanto não pode haver nenhum elemento no conjunto B que receba duas flechas.



Função Bijetora: é quando é injetora e sobrejetora ao mesmo tempo.