f(x)=ax²+bx+c onde a, b e c são constantes reais,
sendo que Dom(f)=R, Im(f)=R.
Esta função também é denominada função trinômia do segundo grau, uma vez que a expressão
a x² + b x + c = 0 representa uma equação do segundo grau. O gráfico cartesiano desta função polinomial do segundo grau é uma curva plana denominada parábola.
Dentre as dezenas de aplicações da parábola a situações da vida, as mais importantes são:
Faróis de carros: Se colocarmos uma lâmpada no foco de um espelho com a superfície parabólica e esta lâmpada emitir um conjunto de raios luminosos que venham a refletir sobre o espelho parabólico do farol, os raios refletidos sairão todos paralelamente ao eixo que contem o "foco" e o vértice da superfície parabólica. Esta é uma propriedade geométrica importante ligada à Ótica, que permite valorizar bastante o conceito de parábola no âmbito do Ensino Fundamental.
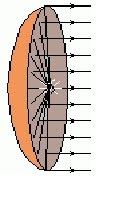
Antenas parabólicas: Se um satélite artificial colocado em uma órbita geoestacionária emite um conjunto de ondas eletromagnéticas, estas poderão ser captadas pela sua antena parabólica , uma vez que o feixe de raios atingirá a sua antena que tem formato parabólico e ocorrerá a reflexão desses raios exatamente para um único lugar, denominado o foco da parábola, onde estará um aparelho de receptor que converterá as ondas eletromagnéticas em um sinal que a sua TV poderá transformar em ondas que por sua vez significarão filmes, jornais e outros programas que você assiste normalmente.
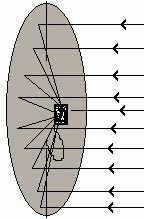
Radares: Os radares usam as propriedades óticas da parábola, similares às citadas anteriormente para a antena parabólica e para os faróis.
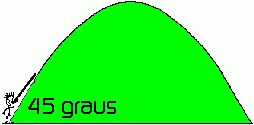
Lançamentos de projéteis: Ao lançar um objeto no espaço (dardo, pedra, tiro de canhão) visando alcançar a maior distância possível tanto na horizontal como na vertical, a curva descrita pelo objeto é aproximadamente uma parábola, se considerarmos que a resistência do ar não existe ou é pequena.
Nenhum comentário:
Postar um comentário